jak obliczyć pole obszaru ograniczonego krzywymi?
Justyna2592: Oblicz pole obszaru ograniczonego krzywymi y= −3x
2 i y= 2x−1

30 sie 19:47
30 sie 21:02
Beti:
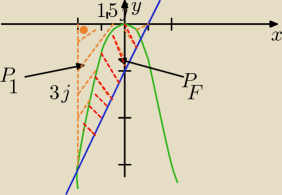
| | 1 | | 3 | | 9 | |
PΔ = |
| * |
| *3 = |
| −−> pole trójkata prostokątnego, którego przeciwprostokątna |
| | 2 | | 2 | | 4 | |
zawiera się w prostej y = 2x−1
| | x3 | | 1 | |
P1 = −∫1/2−1(−3x2)dx = [3* |
| ]1/2−1 = [x3]1/2−1 = |
| − (−1) = |
| | 3 | | 8 | |
pole obszaru ograniczonego krzywymi jest więc równe:
| | 9 | | 9 | | 9 | |
PF = PΔ − P1 = |
| − |
| = |
| |
| | 4 | | 8 | | 8 | |
Co prawda od bardzo dawna nie robiłam takich zadań, ale wydaje mi się, że tak należy je zrobić

30 sie 21:03
Beti: no i już widzę, że namieszałam z tym trójkącikiem po prawej stronie

30 sie 21:05
Justyna2592: A mógłby mi ktoś pokazać krok po kroku jak to robić bo mam takie zadanie na egzaminie a nie mam
zielonego pojęcia jak coś takiego się robi...
30 sie 21:10
Krzysiek: najlepiej zaczynać od rysunku (chociaż nie zawsze jest to konieczne)
szukasz granicę całkowania dla 'x' czyli znajdujesz punkty wspólne krzywych następnie z rysunku
patrzysz która krzywa przyjmuje większe wartości (która jest 'nad' drugą krzywą) i liczysz
całkę:
∫ab (f(x)−g(x) )dx
gdzie f(x) przyjmuje większe wartości w przedziale [a,b]
[a,b] −granice całkowania dla 'x'
30 sie 21:15



